I sottoinsiemi

Per questa lezione consiglio il seguente percorso:

1) leggi questo post
2) esercitati con Genially (lo trovi al termine delle spiegazioni)
3) allenati svolgendo esercizi con i Moduli di Google (fai clic su questo link)
4) verifica il tuo apprendimento on line su questo blog (vedi al termine del post) oppure a questo link
5) Se preferisci puoi svolgere gli esercizi in forma cartacea e controllare le tue risposte con le soluzioni proposte

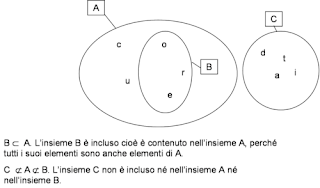
Consideriamo ora questi insiemi e rappresentiamoli graficamente:

A = {a/a è lettera della parola cuore}

B = {b/b è una lettera della parola ore}

C = {c/c è una lettera della parola dati}

Possiamo dire che l'insieme B è un sottoinsieme proprio dell'insieme A perchè ogni elemento di B appartiene ad A, ma c'è almeno un elemento di A che non appartiene a B. Sono invece sottoinsiemi impropri l'insieme vuoto Æ e l'insieme A stesso.

Consideriamo ora un insieme A:

A = {Luca; Marco; Giorgio}

Vediamo quali sono i suoi possibili sottoinsiemi:

{ {Luca}; {Marco}; {Giorgio}; {Luca; Marco}; {Luca; Giorgio}; {Marco; Giorgio}; {Luca; Marco; Giorgio}; Æ}

I primi sei sono i sottoinsiemi propri, mentre gli altri due sono sottoinsiemi impropri.

Se indico con B uno qualsiasi di questi sottoinsiemi, con la scrittura

B Ì A indico uno qualsiasi dei sottoinsiemi propri di A mentre con la scrittura

B Í A (si legge " B contenuto o uguale ad A) indico uno qualsiasi dei sottoinsiemi di A.

L'INSIEME DELLE PARTI

L'insieme formato da tutti i possibili sottoinsiemi propri ed impropri di A si chiama insieme delle parti di A e si indica con Ã(A) .

Se abbiamo

A = {a/a è una vocale della parola paperone}

l'insieme Ã(A) sarà (notate che i primi due sottoinsiemi sono impropri, gli altri sono propri):

Ã(A) = {Æ; {a;e;o}; {a}; {e}; {0}; {a;e}; {a;o}; {e;o} }

LA PARTIZIONE DI UN INSIEME 

Cosa significa fare una partizione in un insieme? Consideriamo l'insieme A formato da alcune regioni italiane:

A = {Piemonte; Liguria; Veneto; Toscana; Marche; Puglia; Campania; Calabria} e formiamo tre sottoinsiemi:

B = {b/b è una regione dell'Italia Settentrionale}

C = {c/c è una regione dell'Italia Centrale}

D = {d/d è una regione dell'Italia Meridionale}

Per elencazione avremo:

B = {Piemonte; Liguria; Veneto}

C = {Toscana; Marche}

D = {Puglia; Campania; Calabria}

Osserviamo le caratteristiche di questi sottoinsiemi:

• Non ci sono elementi in comune tra i sottoinsiemi (infatti, se una regione appartiene, ad esempio, all'Italia Centrale, non può appartenere anche all'Italia Settentrionale)
• Nessuno di questi sottoinsiemi è vuoto.
• Riunendo i sottoinsiemi otteniamo di nuovo l'insieme di partenza A.

In questo caso abbiamo fatto una partizione dell'insieme A.
Operare una partizione dell'insieme significa dunque suddividerlo in due o più sottoinsiemi che devono rispettare queste condizioni:
- non devono avere elementi in comune
- non devono essere vuoti
- riuniti tutti i sottoinsiemi, si deve ottenere l'insieme di partenza.

Puoi seguire questa lezione ed esercitarti anche on line, con Genially. 

Ecco una serie di esercizi che puoi svolgere on line seguiti da esercizi in forma cartacea.

ESERCIZI DA STAMPARE

1. Stabilisci quali dei seguenti insiemi sono sottoinsiemi dell'insieme A:

A = {a/a è un pesce}

B = {trota; carpa; tinca; sogliola}

C = {orata; squalo; rondine; cane}

D = {sardina; acciuga; pesce spada; branzino}

E = {trota; orata; acciuga; alga}

2. Spiega il significato delle seguenti notazioni e rappresentale graficamente

• X Ì Z
• X Ì Z ÌY
• X Ì Z - Y Ì Z - Y Ë X

3. Rappresenta per elencazione tutti i possibili sottoinsiemi propri dell'insieme A = {a; b; c}. Quanti sono?

4. Rappresenta per elencazione tutti i possibili sottoinsiemi propri ed impropri dell'insieme A = {2; 4; 6}. Quanti sono?

5. Dato l'insieme A = {uva; mela; pera} individua tra i seguenti qual è l'insieme delle parti di A
- Ã(A) = {Æ; {uva}; {mela}; {pera}; {uva; mela}; {uva; pera}; {mela; pera}; {uva;mela; pera} }.
- Ã(A) = { {uva}; {mela}; {pera}; {uva; mela}; {uva; pera}; {mela; pera} {uva;mela; pera} }.
- Ã(A) = {Æ; {uva}; {mela}; {pera}; {uva; mela}; {uva; pera}; {mela; pera} }.

6. Perchè gli insiemi A = {1; 2; 3; 4} e C = {3; 4; 5; 6} non sono una partizione dell'insieme X = {1; 2; 3; 4; 5; 6}?

7. Esegui la partizione del seguente insieme sulla base del numero di lettere da cui è formata ogni parola e poi rappresenta la partizione graficamente:

A = {ago; reo; vai; nemo; topo; rosa; mano; amaro; acido}

Scarica e stampa gli esercizi