Consideriamo una situazione problematica di questo tipo.
Per riscaldare 30
camere di un ospedale per 10 giorni sono stati consumati 90 quintali di
gasolio. Quanti quintali di gasolio si consumeranno per riscaldare 25 camere
per 18 giorni?
Vediamo come in questo caso la grandezza incognita non
dipende solo da un’altra grandezza, dipende da più grandezze. I problemi di
questo tipo si chiamano problemi del tre
composto perché possiamo considerarli composti da due o più problemi del
tre semplice.
Mettiamo i dati in una tabella:
n° camere
|
n° giorni
|
quintali di gasolio
|
30
|
10
|
90
|
25
|
18
|
x
|
Suddividiamo il problema in due problemi del tre semplice,
considerando solo due grandezze variabili e mantenendo costante la terza.
Se manteniamo costanti i giorni, avremo
n° camere
|
n° giorni
|
quintali di gasolio
|
30
|
10
|
90
|
25
|
10
|
x
|
Tralasciamo la grandezza costante. La nostra tabella diventa
così, considerando che le due grandezze sono direttamente proporzionali.
75 saranno i quintali di gasolio necessari per riscaldare 25
camere per 10 giorni.
Manteniamo ora costante il numero delle camere. E’ come se
il nostro problema fosse diventato: “Per
riscaldare 25 camere per 10 giorni si consumano 75 quintali di gasolio. Quanti
quintali si consumeranno per riscaldare 25 camere per 18 giorni?”. Avremo
dunque:
n° camere
|
n° giorni
|
quintali di gasolio
|
25
|
10
|
75
|
25
|
18
|
x
|
Tralasciamo la grandezza costante. La nostra tabella diventa
così, considerando che le due grandezze sono direttamente proporzionali.
135 saranno i quintali di gasolio necessari per riscaldare
25 camere per 18 giorni.
C’è però la possibilità
di usare un procedimento più veloce.
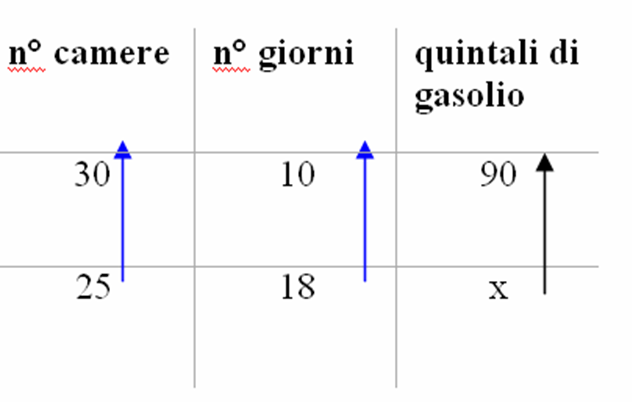
Ripartiamo dalla tabella iniziale e disegniamo una freccia
che va dalla x verso il valore conosciuto.
Stabiliamo poi se ogni grandezza è direttamente o
inversamente proporzionale rispetto alla grandezza con l’incognita (nel nostro
esempio sia la grandezza “n° camere” sia “n° giorni” sono direttamente
proporzionali alla grandezza “quintali di gasolio”). Se le grandezze sono
direttamente proporzionali disegniamo per ogni grandezza una freccia con lo
stesso verso di quella già tracciata, se sono inversamente proporzionali
disegniamo una freccia di verso opposto.
Potremo ora
calcolare il valore di x moltiplicando il valore noto 90 per le altre grandezze
seguendo il verso delle frecce.
Consideriamo questa situazione problematica
Un lingotto d’oro
lungo 39 mm, largo 22 mm e spesso 1,3 mm pesa 21 grammi.
Un altro lingotto
d’oro è lungo 45 mm, largo 25 mm e pesa 50 grammi. Qual è il suo spessore?
Mettiamo i dati in tabella e tracciamo una freccia dalla x
al valore noto.
ESERCIZI
·
Un
automobilista che viaggia 6 ore al giorno alla velocità media di 110 km/h
impiega 4 giorni a compiere un certo percorso. Quanto tempo impiegherebbe a
fare lo stesso percorso viaggiando 4 ore al giorno alla velocità di 120 km/h?
·
Una
lastra di rame lunga 1,5 m , larga 1,2 m e spessa 2,5 mm pesa 40 kg. Quanto
peserà un’altra lastra di rame lunga 2 m, larga 0,6 m e spessa 3 mm?
·
In
un’azienda 40 operai lavorano 8 ore al giorno producendo 2500 kg di merce in 25
giorni. Quanti giorni impiegheranno 50 operai che lavorano 6 ore al giorno per
produrre 3000 kg di merce?
·
Per
riempire un piccolo bacino del volume di 180 m3 5 pompe di
sollevamento impiegano 15 ore. Quante ore impiegheranno 8 pompe della stessa
portata per riempire un bacino di 240 m3?