ANGOLI ALLA
CIRCONFERENZA
Premetto che gli archi e gli angoli dovrebbero essere
indicati così:
Per comodità non userò questa notazione, incompatibile con
la piattaforma di Blogger.
Consideriamo una circonferenza di raggio r e di centro O. Su di essa
stabiliamo un punto P e da esso facciamo partire due semirette qualsiasi che
incontrino la circonferenza nei due punti A e B. Si determina così un arco AB
ed un angolo convesso α.
L’ angolo convesso α
si chiama angolo alla circonferenza che insiste sull’arco AB.
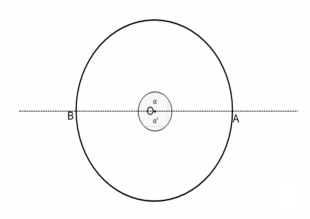
Consideriamo ora un cerchio
di raggio r e di centro O. Facciamo partire dal centro O due semirette
qualsiasi che incontrano la circonferenza nei due punti A e B. Si determinano
così due archi e due angoli, convesso α e concavo α’.
I due angoli α e α’ sono esplementari perché la loro somma è
360°.
Esaminiamo ora due casi particolari di angoli al centro:
Se l’angolo al centro è originato da due semirette
perpendicolari, l’angolo al centro α sarà retto e insisterà sull’arco AB che è
la quarta parte della circonferenza.
Se l’angolo al centro è determinato da due semirette
adiacenti, quindi dal diametro, gli angoli al centro α e α’ saranno piatti ed
insisteranno su archi corrispondenti alla semicirconferenza.
Vediamo ora alcune proprietà legate agli angoli al centro o
alla circonferenza.
I due angoli al centro α e α’
insistono rispettivamente sui due archi AB e CD non coincidenti e congruenti
tra loro (AB@CD):
gli angoli al centro α e α’ sono anch’essi congruenti. Possiamo quindi dire che
due angoli al centro sono congruenti se
insistono su archi congruenti.
Dato un arco AB, tutti gli angoli
alla circonferenza che insistono sul suddetto arco sono tra loro congruenti (α@β@γ).
Possiamo quindi affermare che tutti gli angoli alla circonferenza che
insistono sullo stesso arco sono congruenti.
Dato l’angolo alla circonferenza
α che insiste sull’arco AB e l’angolo
alla circonferenza β che insiste sull’arco CD, se gli archi AB e CD sono
congruenti e non coincidenti gli angoli α e β sono congruenti (α@β).
Possiamo dunque affermare che due angoli
alla circonferenza che insistono su due archi congruenti sono anch’essi
congruenti.
Consideriamo un arco AB, l’angolo al centro α che insiste
sull’arco AB e l’angolo β, uno qualsiasi degli angoli alla circonferenza
corrispondenti all’arco AB. L’angolo α è il doppio dell’angolo β (α=2 β).
Possiamo dunque dire che in una
circonferenza l’angolo al centro che insiste su un arco è sempre il doppio di
qualsiasi angolo alla circonferenza che insiste sullo stesso arco.
ESERCIZI
·
Completa
la tabella, sapendo che α è l’angolo al centro e β il corrispondente angolo
alla circonferenza.
α
|
β
|
47°32’
|
|
65°
|
|
51°26’
|
|
27°18’
|
·
Un angolo
al centro insiste su una semicirconferenza. Quanto è ampio? Quanto è ampio il
corrispondente angolo alla circonferenza?
·
Un angolo
alla circonferenza misura 20°; quanto misura il corrispondente angolo al
centro? Su quale parte di circonferenza insiste?
·
Un angolo
alla circonferenza insiste su un arco uguale a 1/3 della circonferenza. Quanto
è ampio?
·
Osserva
la seguente figura: sapendo che l’arco CD è pari ai 2/5 della circonferenza,
calcola l’ampiezza degli angoli del quadrilatero ACBD.
Visualizza, scarica e stampa gli esercizi (word, pdf)Visualizza, scarica e stampa le soluzioni (word, pdf)