Le rette nello spazio
Iniziando ad occuparci della geometria delle figure solide
cominciamo a considerare le rette nello spazio. Possiamo avere diversi casi:
a) rette
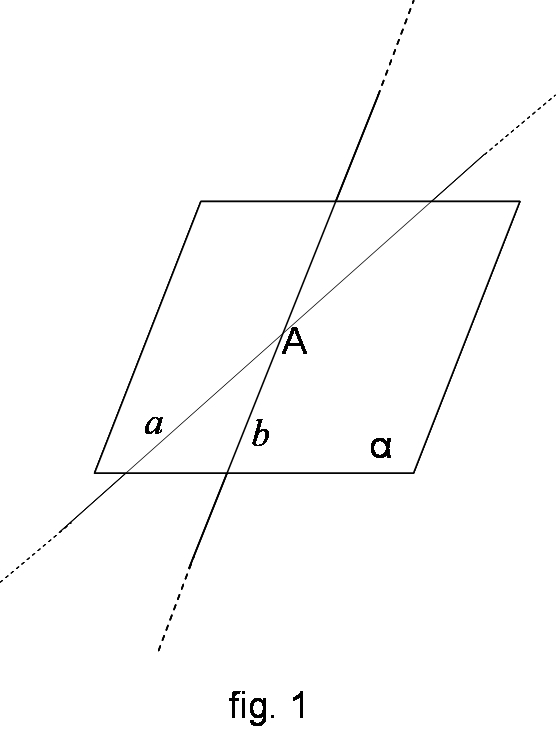
complanari, cioè appartenenti ad uno
stesso piano, che possono avere un punto in comune e si dicono allora incidenti (fig. 1) o non avere nessun
punto in comune e si dicono allora parallele
(fig. 2).
b) rette
non appartenenti allo stesso piano e che non hanno alcun punto in comune si
dicono sghembe (fig. 3).
Nel caso di
rette sghembe possiamo dire che:
I piani nello spazio
Due diversi piani nello spazio possono essere incidenti o secanti se hanno una retta
in comune
Due diversi piani nello spazio possono essere paralleli se non hanno alcun punto in
comune
Per un punto passano infiniti piani.
Per una retta passano infiniti piani.
Per tre punti non allineati passa un solo piano.
Per una retta e un punto non appartenente ad essa passa un
solo piano.
Per due rette incidenti passa un solo piano. Per due rette parallele passa un solo piano.
Consideriamo ora un piano α ed un punto P non appartenente
ad esso: dal punto P tracciamo la perpendicolare p al piano α che incontra il piano nel punto S, notiamo che gli
angoli che forma con tutte le rette del piano α passanti per S sono retti. Il
punto S è il piede della perpendicolare ed il segmento PS è la distanza del punto P al piano α.
Visualizza, scarica e stampa gli esercizi (in word, in pdf)
Visualizza, scarica e stampa le soluzioni (in word, in pdf)