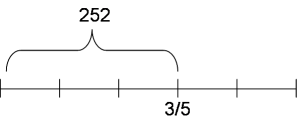Cominciamo con l’esame dei problemi diretti che riguardano il calcolo del valore della
frazione di un numero. Vediamo questo esempio: i ciclisti hanno già percorso i 3/5 di una
tappa lunga 215 km. Quanti km hanno già percorso?
In questo problema dobbiamo operare sul numero 215 con la
frazione 3/5, perciò dobbiamo dividere 215 per il denominatore e moltiplicare
il risultato per il numeratore.
(215 : 5) x 3
Si ottiene lo stesso
risultato moltiplicando il numero dato per la frazione
Vediamo ora i problemi di tipo inverso nei quali, conosciuto il valore di una frazione
di un numero, occorre calcolare quel numero.
Vediamo un esempio: in un teatro sono occupati dagli spettatori i 3/5 dei posti,
cioè 252 posti. Quanti sono tutti i posti del teatro?
Rappresentiamo il numero da trovare con un segmento e su di
esso individuiamo i 3/5 corrispondenti a 252 posti.
Dividendo 252 in 3 parti troviamo il valore di 1/5.
Moltiplicando il risultato per 5 troviamo il valore di 5/5,
cioè il numero dei posti del teatro.
(252 : 3) x 5 = 420
Abbiamo diviso per il numeratore e moltiplicato il risultato
per il denominatore.
Si
ottiene lo stesso risultato dividendo il numero dato per la frazione
Consideriamo ora i problemi che ci chiedono di calcolare due numeri sapendo la loro
somma e che uno è una frazione data dell’altro.
Vediamo un esempio: Luigi compie un viaggio percorrendo in totale 2600 km.
Sapendo che i km che ha percorso in treno sono i 3/5 dei chilometri percorsi in
auto, quanti chilometri ha percorso con ciascuno dei due mezzi di trasporto?
Se i chilometri percorsi in treno sono i 3/5 dei chilometri percorsi in
auto, questi ultimi saranno i 5/5. Rappresentiamo graficamente.
Vediamo che la somma è rappresentata da 8 segmenti uguali,
ciascuno dei quali è 1/8 di 2600, per cui:
(2600 : 8) x 3 = 975 km
(2600 : 8) x 5 = 1 625 km
Possiamo quindi dire che, in casi come questo, occorre dividere la somma per la somma tra
numeratore e denominatore della frazione e poi moltiplicare il quoziente
ottenuto una volta per il numeratore ed una volta per il denominatore.
Vediamo infine i problemi che ci chiedono di calcolare due numeri sapendo la loro differenza
e che uno è una frazione data dell’altro.
Vediamo un esempio: In un parcheggio il numero dei posti per le auto è i 5/2 del
numero dei posti per i camper. Se il numero dei posti per le auto supera di 30
unità il numero dei posti per i camper, quale sarà rispettivamente il numero
dei posti per le auto e quello dei posti per i camper?
Se i posti per le auto sono i 5/2 dei posti per i camper,
questi ultimi saranno i 2/2. Rappresentiamo graficamente.
Vediamo che la differenza è formata da 3 parti uguali, ciascuna delle quali è 1/3 di
30, per cui:
(30 : 3) x 2 = 20 posti per i camper
(30: 3) x 5 = 50 posti per le auto
Possiamo quindi dire che, in casi come questo, occorre dividere la differenza per la differenza
tra i termini della frazione e poi moltiplicare il quoziente ottenuto una volta
per il numeratore ed una volta per il denominatore.
ESERCIZI
·
L’età di Marco è i 3/7 di quella del padre che
ha 42 anni. Quanti anni ha Marco?
·
In una classe di 25 alunni i 3/5 sono maschi, i
2/5 delle ragazze hanno gli occhiali. Quante sono le ragazze senza occhiali?
·
Il papà di Luca ha uno stipendio mensile di € 1
660. Se ogni mese spende i 2/5 per l’affitto ed i 2/3 di ciò che rimane per il
vitto, quanto gli rimane per le altre spese?
·
Per l’acquisto di un appartamento la famiglia di
Giorgio versa come acconto € 45 000, corrispondenti ai 3/14 del prezzo totale.
Quanto costa l’appartamento?
·
In una teatro vi sono 255 posti in platea, che
rappresentano i 5/7 di tutti i posti del teatro. Se sono occupati da spettatori
i 4/7 di tutti i posti del teatro, quanti sono i posti rimasti liberi?
·
In un terreno sono stati piantati
complessivamente 234 alberi, tra peschi ed albicocchi. Se gli albicocchi sono i
5/8 dei peschi, quanti sono rispettivamente gli alberi di pesco e di albicocco?
·
Tra Giorgio e Luca ci sono 15 anni di
differenza. L’età di Giorgio è i 5/2 di quella di Luca. Quanti anni hanno
rispettivamente Giorgio e Luca?
·
Il segmento AB misura 18 cm ed è pari ai 3/7 del
segmento CD. Quale sarà la lunghezza di un altro segmento EF pari ai 5/6 della
differenza fra le lunghezze dei segmenti AB e CD?