Per questa lezione consiglio il seguente percorso:
2) esercitati con Genially (lo trovi al termine delle spiegazioni)
3) verifica il tuo apprendimento on line su questo blog (vedi al termine del post) oppure a questo link
5) Se preferisci puoi svolgere gli esercizi in forma cartacea e controllare le tue risposte con le soluzioni proposte
La geometria studia la forma, la grandezza e la posizione dei corpi materiali.
Gli enti geometrici fondamentali sono tre: il punto, la retta ed il piano. Essi costituiscono delle astrazioni.
Cominciamo dal punto geometrico: non ha alcuna grandezza, ma solo una posizione. Si indica con le lettere maiuscole dell’alfabeto.

Un insieme infinito e continuo di punti che hanno sempre la stessa direzione costituisce una retta. Come già il punto, anche la retta non esiste nella realtà materiale perché non ha né spessore né larghezza. L’unica dimensione della retta è la lunghezza. Si indica con le lettere minuscole dell’alfabeto.
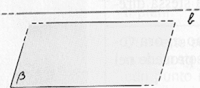
Vediamo ora il piano, anche questo non esistente nella realtà concreta, perché è un insieme continuo ed infinito di rette, privo di spessore, con due sole dimensioni: lunghezza e larghezza. Per indicarlo si usano le lettere minuscole dell’alfabeto greco (α, β, δ, ....).
Cerchiamo di capire ora alcune proprietà degli enti fondamentali.
Per un punto A passano infinite rette.
Per due punti distinti A e B passa una sola retta.
Per tre punti distinti passa una sola retta, solo se i tre punti sono allineati.
Per una retta passano infiniti piani
Per tre punti non allineati passa un solo piano.
Vediamo quali possono essere le posizioni reciproche di due rette.
La retta t e la retta s appartengono al piano α (s, t ∈ α). Infatti l’insieme dei punti della retta s e l’insieme dei punti della retta t sono inclusi nel piano α
{s} {t} ⊂ {α}.
L’intersezione tra la retta s e la retta t (ciò che hanno in comune) è costituita dal punto Q.
{s} ∩ {t} = Q.
Le due rette sono quindi incidenti perché appartengono allo stesso piano ed hanno un punto in comune.
La retta c appartiene al piano γ mentre la retta d non appartiene al piano γ (c ∈ γ; d ∉ γ). Infatti l’insieme dei punti della retta c è incluso nel piano γ mentre l’insieme dei punti della retta d non è incluso nel piano γ
{c} ⊂ {γ}; {d} ⊄ {γ}.
L’intersezione tra la retta c e la retta d (ciò che hanno in comune) è un insieme vuoto.
{c} ∩ {d} = ∅.
Le due rette sono quindi sghembe perché non appartengono allo stesso piano e non hanno alcun punto in comune.
La retta a e la retta b appartengono al piano β (a, b ∈ β). Infatti l’insieme dei punti della retta a e l’insieme dei punti della retta b sono inclusi nel piano β.
{a} {b} ⊂ {β}.
L’intersezione tra la retta a e la retta b (ciò che hanno in comune) è un insieme vuoto.
{a} ∩ {b} = ∅.
Le due rette sono quindi parallele perché appartengono allo stesso piano e non hanno alcun punto in comune.
Il postulato delle parallele: considerata una retta ed un punto non appartenente alla retta, per quel punto passa una sola retta parallela a quella data.
Se consideriamo una retta ed un piano e le loro posizioni reciproche possiamo avere queste situazioni:
La retta a giace nel piano α. La retta a appartiene al piano α (a ∈ α). Infatti l’insieme dei punti della retta a è incluso nel piano α.
{a} ⊂ {α}.
L’intersezione tra la retta ed il piano (ciò che hanno in comune) è costituita dalla retta stessa {a} ∩ {α} = a.
{a} ⊂ {α}.
L’intersezione tra la retta ed il piano (ciò che hanno in comune) è costituita dalla retta stessa {a} ∩ {α} = a.
La retta b è parallela al piano β. La retta b non appartiene al piano β (b ∉ β). Infatti l’insieme dei punti della retta b non è incluso nel piano β.
{b} ⊄ {β}.
L’intersezione tra la retta ed il piano (ciò che hanno in comune) è un insieme vuoto {b} ∩ {β} = ∅.
La retta d è incidente al piano δ. La retta d non appartiene al piano δ (d ∉ δ). Infatti l’insieme dei punti della retta d non è incluso nel piano δ.
{d} ⊄ {δ}.
L’intersezione tra la retta ed il piano (ciò che hanno in comune) è il punto P {d} ∩ {δ} = P.
{d} ⊄ {δ}.
L’intersezione tra la retta ed il piano (ciò che hanno in comune) è il punto P {d} ∩ {δ} = P.
Puoi seguire questa lezione ed esercitarti anche on line, con Genially.
Ecco una serie di esercizi che puoi svolgere on line seguiti da esercizi in forma cartacea.
ESERCIZI
- Quante e quali dimensioni ha la retta?
- Quante rette passano per un punto?
- Quante rette passano per due punti?
- Quante e quali dimensioni ha il piano?
- Disegna tre punti A, B e C in un piano δ, in modo che ci sia una sola retta che li unisca. Come devono essere i tre punti?
- Disegna tre rette a, b, c appartenenti allo stesso piano e che godano di queste proprietà
a ∩ b ∩ c = ∅
Come sono tra loro le rette?
- Guarda la figura e completa le uguaglianze
a ∩ b = …..
d ∩ c = …..
a ∩ d = …..
b ∩ c = …..