Abbiamo già visto
che i prismi sono quei poliedri che hanno almeno due facce parallele e
congruenti.
Le facce parallele e
congruenti sono le basi del prisma, le altre facce sono
parallelogrammi e si dicono facce laterali; la distanza fra le due basi è l’altezza del prisma.
Un prisma può
essere triangolare se il poligono di
base è un triangolo, quadrangolare se
il poligono di base è un quadrilatero, pentagonale
se il poligono di base è un pentagono e così via.
I prismi come quello
a sinistra, in cui tutte le facce laterali sono perpendicolari alla base,
vengono chiamati prismi retti e le loro facce laterali sono
rettangoli mentre l’altezza coincide con gli spigoli laterali, i prismi come
quello a destra vengono chiamati prismi
obliqui e le loro facce sono
dei parallelogrammi.
Un prisma può essere
regolare se è retto e i poligoni di
base sono poligoni regolari: in questo caso le facce laterali sono rettangoli
congruenti.
Superficie laterale
Consideriamo un prisma triangolare retto ed il suo sviluppo.
Notiamo che la superficie laterale del prisma coincide con
la superficie di un rettangolo, la cui base è congruente al perimetro di base
del prisma e la cui altezza è congruente all’altezza del prisma.
Possiamo dunque affermare che la superficie laterale di un prisma retto si calcola moltiplicando il
perimetro di base per la misura dell’altezza.
Sl = p . h
Dalla formula diretta possiamo ricavare le formule inverse:
p = Sl/h h
= Sl/p
Superficie totale
E’ abbastanza evidente che l’area della superficie totale
sarà data dalla somma dell’area della superficie laterale e dell’area delle due
basi.
St = Sl + 2Ab
Dalla formula diretta possiamo ricavare le formule inverse:
Sl = St - 2Ab Ab
= (St – Sl)/2
Volume
Misurare il volume di un solido significa calcolare quante
volte l’unità di misura del volume scelta è contenuta nel solido.
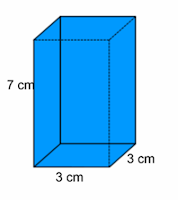
Guardiamo questo prisma retto a base quadrata:
l’area di base è di 9 cm2 quindi per ricoprire la
base occorreranno 9 cm2.
Quanti strati di cm2 saranno necessari per
occupare tutto lo spazio del nostro prisma? 7 strati perché l’altezza è di 7
cm.
Il volume del nostro solido misurerà quindi 63 cm3
(3 x 3 x 7).
Abbiamo prima calcolato l’area della base e poi abbiamo moltiplicato
per l’altezza.
Il volume di un
prisma retto si calcola moltiplicando l’area di base per la misura
dell’altezza.
V = Ab . h
Dalla formula diretta possiamo ricavare le formule inverse:
Ab = V/h h
= V/ Ab
ESERCIZI
·
Un prisma retto ha per base un quadrato la cui
area è 225 cm2. L’altezza del prisma è di 26 cm. Calcola l’area
della sua superficie totale.
·
Un prisma retto ha per base un triangolo
rettangolo con il cateto minore di 100 cm ed il cateto maggiore che è i 21/20
del cateto minore. Sapendo che il prisma è alto 130 cm, calcola l’area della
superficie totale ed il volume.
·
Un prisma retto, di volume 5400 cm3,
ha per base un rombo avente la diagonale minore e il lato lunghi
rispettivamente 18 cm e 15 cm. Calcola l’area della superficie totale.